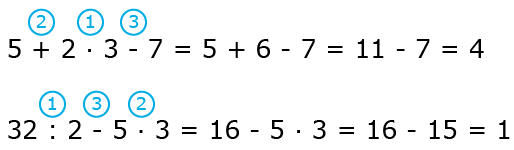Порядок действий в математике, последовательность выполнения умножения, сложения, деления, вычитания, правила очередности арифметических действий

Основные операции в математике

Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).

Операции действия:

• сложение (+)
• вычитание (-)
• умножение (*)
• деление (:)

Операции отношения:

• равно (=)
• больше (>)
• меньше (<)
• больше или равно (≥)
• меньше или равно (≤)
• не равно (≠)

Сложение — операция, которая позволяет объединить два слагаемых.

Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.

Вычитание — действие, обратное сложению.

Запись вычитания: 10 – 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.

Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 – 1 = 9.

Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.

• Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.
• 3 * 4 = 3 + 3 + 3 + 3

В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 * 2 = 5 + 5 = 10.

Поэтому и множитель, и множимое называют сомножителями.

Деление — арифметическое действие обратное умножению.

Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.

В этом случае произведение делителя 6 и частного 5, в качестве проверки, дает делимое 30.

Если в результате операции деления, частное является не целым числом, то его можно представить в виде дроби.

Возведение степень — операция умножения числа на самого себя несколько раз.

Основание степени — число, которое повторяется сомножителем определённое количество раз.

Показатель степени — число, которое указывает, сколько раз берется одинаковый множитель.

Степенью называется число, которое получается в результате взаимодействия основания и показателя степени.

• Запись: 34 = 81, где 3 — основание степени, 4 — показатель степени, 81 — степень.
• 3^4 = 3 * 3 * 3 * 3

Вторая степень называется квадратом, третья степень — кубом. Первой степенью числа называют само это число.

Извлечение корня — арифметическое действие, обратное возведению в степень.

• Запись: 4√81 = 3, где 81 — подкоренное число, 4 — показатель корня, 3 — корень.
• З^4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
• 2√16 = 4 — корень второй степени называется — квадратным.

При знаке квадратного корня показатель корня принято опускать: √16 = 4.

3√8 = 2 — корень третьей степени называется — кубическим.

Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно представляют обратные друг другу действия. Далее узнаем порядок выполнения арифметических действий.

Что такое действия первой и второй ступени

Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).

Сложение и вычитание

Какие же действия можно произвести с числами? Есть два базовых. Это сложение и вычитание. Все остальные действия построены на этих двух.

Самое простое человеческое действие: взять две кучки камней и смешать их в одну. Это и есть сложение. Для того чтобы получить результат такого действия, можно даже не знать, что такое сложение. Достаточно просто взять кучку камней у Пети и кучку камней у Васи. Сложить все вместе, посчитать все заново. Новый результат последовательного счета камней из новой кучки − это и есть сумма.

Точно так же можно не знать, что такое вычитание, просто взять и разделить кучу камней на две части или забрать из кучи какое-то количество камней. Вот и останется в куче то, что называется разностью. Забрать можно только то, что есть в куче. Кредит и прочие экономические термины в данной статье не рассматриваются.

Чтобы не пересчитывать каждый раз камни, ведь бывает, что их много и они тяжелые, придумали математические действия: сложение и вычитание. И для этих действий придумали технику вычислений.

Сумма двух любых цифр тупо заучиваются без всякой техники. 2 плюс 5 равно семь. Посчитать можно на счетных палочках, камнях, рыбьих головах – результат одинаковый. Положить сначала 2 палочки, потом 5, а потом посчитать все вместе. Другого способа нет.

Те, кто поумнее, обычно это кассиры и студенты, заучивают больше, не только сумму двух цифр, но и суммы чисел. Но самое главное, они могут складывать числа в уме, используя разные методики. Это называется навыком устного счета.

Для сложения чисел, состоящих из десятков, сотен, тысяч и еще больших разрядов, используют специальные техники − сложение столбиком или калькулятор. С калькулятором можно не уметь складывать даже цифры, да и читать дальше не нужно.

Сложение столбиком −­­­­­­ это метод, который позволяет складывать большие (многоразрядные) числа, выучив только результаты сложения цифр. При сложении столбиком последовательно складываются соответствующие десятичные разряды двух чисел (то есть фактически две цифры), если результат сложения двух цифр превышает 10, то учитывается только последний разряд этой суммы – единицы числа, а к сумме следующих разрядов добавляется 1.

Умножение

Математики любят группировать похожие действия для упрощения расчетов. Так и операция умножения является группировкой одинаковых действий – сложения одинаковых чисел. Любое произведение N x M − есть N операций сложения чисел M. Это всего лишь форма записи сложения одинаковых слагаемых.

Для вычисления произведения используется такой же метод – сначала тупо заучивается таблица умножения цифр друг на друга, а потом применяется метод поразрядного умножения, что называется «в столбик».

Что сначала – умножение или сложение?

Любое математическое выражение – это фактически запись учетчика «с полей» о результатах каких-либо действий. Допустим, сбора урожая помидоров:

• 5 взрослых работников собрали по 500 помидоров каждый и выполнили норму.
• 2 школьников не ходили на уроки математики и помогали взрослым: собрали по 50 помидоров, норму не выполнили, съели 30 помидоров, надкусили и испортили еще 60 помидоров, 70 помидоров было изъято из карманов помощников. Зачем брали с собой их в поле – непонятно.

Все помидоры сдавали учетчику, он укладывал их по кучкам.

Запишем результат «сбора» урожая в виде выражения:

• 500 + 500 + 500 + 500 + 500 – это кучки взрослых работников;
• 50 + 50 – это кучки малолетних работников;
• 70 – изъято из карманов школьников (испорченное и надкусанное в зачет результата не идет).

Получаем пример для школы, запись учетчика результатов работы:

500 + 500 +500 +500 +500 + 50 +50 + 70 =?;

Здесь можно применить группировку: 5 кучек по 500 помидоров − это можно записать через операцию умножения: 5 ∙ 500.

Две кучки по 50 – это тоже можно записать через умножение.

И одна кучка 70 помидоров.

5 ∙ 500 + 2 ∙ 50 + 1 ∙ 70 =?

И что делать в примере сначала − умножение или сложение? Так вот, складывать можно только помидоры. Нельзя сложить 500 помидоров и 2 кучки. Они не складываются. Поэтому сначала нужно всегда все записи привести к базовым операциям сложения, то есть в первую очередь вычислить все операции группировки-умножения. Совсем простыми словами – сначала выполняется умножение, а сложение уже потом. Если умножить 5 кучек по 500 помидоров каждая, то получится 2500 помидоров. А дальше их уже можно складывать с помидорами из других кучек.

2500 + 100 + 70 = 2 670

При изучении ребенком математики нужно донести до него, что это инструмент, используемый в повседневной жизни. Математические выражения являются, по сути (в самом простом варианте начальной школы), складскими записями о количестве товаров, денег (очень легко воспринимается школьниками), других предметов.

Соответственно, любое произведение – это сумма содержимого некоторого количества одинаковых емкостей, ящиков, кучек, содержащих одинаковое количество предметов. И что сначала умножение, а сложение потом, то есть сначала начала вычислить общее количество предметов, а затем уже складывать их между собой.

Деление

Операция деления отдельно не рассматривается, она обратная умножению. Нужно что-то распределить по коробкам, так, чтобы во всех коробках было одинаковое заданное количество предметов. Самый прямой аналог в жизни – это фасовка.

Порядок действий без скобок

Установленный порядок арифметических действий без скобок:

1. Если выражение содержит только действия на сложение и вычитание, то они выполняются в порядке следования — слева направо:
2. Если выражение содержит только действия на умножение и деление, то действия выполняются в порядке следования — слева направо:
3. Если в выражении присутствуют и умножение с делением, и сложение с вычитанием, то сначала выполняются умножение и деление в порядке их следования (слева направо), а затем сложение и вычитание в порядке их следования (слева направо):

Порядок действий со скобками

Если выражение содержит скобки, то сначала выполняются все действия внутри скобок, а затем все действия, находящиеся за скобками.

В числовых выражениях со скобками порядок выполнения арифметических действий такой же, как и в выражениях без скобок.

Скобки применяются для обозначения действий, которые нужно произвести раньше остальных. Скобки не влияют на порядок остальных действий в выражении, остальные действия выполняются в указанном порядке.

Примеры на порядок действий 3-4 класс для тренировки

Рассмотрим выражения, установим порядок действий и выполним вычисления.

Будем действовать по правилу. В выражении 43 – (20 – 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.

43 – (20 – 7) +15 =43 – 13 +15 = 30 + 15 = 45

В выражении 32 + 9 * (19 – 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.

32 + 9 * (19 – 16) =32 + 9 * 3 = 32 + 27 = 59

В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.

Узнаем, правильно ли определен порядок действий в следующих выражениях.

В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.

Найдем значение данного выражения.

Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

Расставим порядок действий в выражении, используя изученное правило (рис. 5).

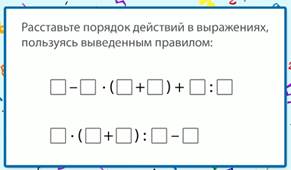
Рис. 5. Порядок действий

Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.

Действуем по алгоритму.

В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.

Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.

Проверим себя (рис. 6).

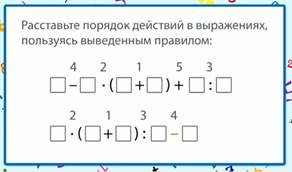
Рис. 6. Порядок действий

Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.

Список литературы

1. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
2. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
3. М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
4. Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
5. «Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
6. С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
7. В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Домашнее задание

Определи порядок действий в данных выражениях. Найди значение выражений.

***

Определи, в каком выражении такой порядок выполнения действий:

• умножение;
• деление;.
• сложение;
• вычитание;
• сложение.

Найди значение данного выражения.

***

Составь три выражения, в которых такой порядок выполнения действий:

• умножение; 2. сложение; 3. вычитание
• сложение; 2. вычитание; 3. сложение
• умножение; 2. деление; 3. сложение

Найди значение этих выражений.

Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.

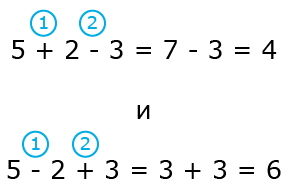
Если несколько действий выполняются одно за другим, то результат, зависит от порядка действий.

Если производить действия в порядке их записи.

Если же сначала сложить 2 и 1 и вычесть полученную сумму из 4, то получим 1.

Чтобы указать, в каком порядке нужно выполнять действия (в тех случаях, когда результат зависит от порядка действий), пользуются скобками. Действия, заключенные в скобки, выполняются раньше других. В нашем случае:

Чтобы не загромождать чрезмерно записи, условились не писать скобок:

• в том случае, когда действия сложения и вычитания, следуя друг за другом, должны выполняться в том порядке, в каком они записаны;
• в том случае, когда внутри скобок производятся действия умножения или деления; например, вместо 2 + (4 · 5) = 22 пишут 2 + 4 · 5 = 22.

При вычислении таких выражений, которые либо совсем не содержат скобок, либо содержат лишь такие скобки, внутри которых больше нет скобок, нужно производить действия в таком порядке:

• сначала выполняются действия, заключенные в скобки; при этом умножение и деление делаются в порядке из следования, но раньше, чем сложение и вычитание;
• затем выполняются остающиеся действия, причем опять умножение и деление делаются в порядке из следования, но раньше сложения и вычитания.

Сначала выполняем умножения:
2 · 5 = 10
3 · 3 = 9
затем вычитание:
10 – 9 = 1

Сначала выполняем действия в скобках:
16 – 2 · 7 + 4 = 16 – 14 + 4 = 6
2 + 5 = 7

Теперь выполняем остающиеся действия:
9 + 16 : 4 – 2 · 6 + 6 · 7 =
= 9 + 4 – 12 + 42 =
= 43

Часто для указания порядка действий необходимо заключать в скобки такие выражения, которые сами уже содержат скобки. Тогда, кроме обычных (круглых), применяют скобки иной формы, например квадратные []. Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками <>. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.

Выполняем действия в круглых скобках, имеем:
8 – 6 = 2
10 – 2 · 3 = 10 – 6 = 4

действия в квадратных скобках дают:
14 – 3 · 2 = 8

выполняя остающиеся действия скобках находим:
5 + 2 · 8 + 32 : 4 = 5 + 16 + 8 = 29

Порядок действий:
30 – 20 = 10
35 – 10 = 25
100 – 25 = 75
75 · 2 = 150

Расставь порядок действий. Найди значение выражения:

1. (12 – 0 : 4) : 3 – (7 – 7)*45 + (36 : 6) : (15 : 15)
2. 36 : (12 – 6 : 20 – (0 *5 + 3) – (7 * 8) : 14 : 4
3. (3 + 27 : 3) * 5 – 60 * 3 : 90 + 8 * (7 – 7) : 4
4. (630 : 7 + 4 * 9) : (5 + 5 : 5) + (8 – 8) : (35 * 7 + 49)
5. 5 * (48 : 6 + 2 : 2) – 280 : 20 * 3 + (50 – 32) : 9
6. 8040 : 6 + (109004 – 76048) : 7
7. (64000 : 80 * 3 + 600) : 15 – (3200 * 100) : 2000
8. 240400 – (5796 + 1803200 : 400) * 8
9. 345 * (250 * 125) * (8 * 400)
10. 56432 : 8 * 50 – (223956 + 882630 : 9)
11. (62456715 + 548185) : 700 – 300 * 80450 : 5000
12. 80 – (17 * 4) : (20 – 380 : 20) + 90 * 40 : 120
13. (1000 – 999) * 40 – 0 : 24 + 360 : (16 * 5 + 280 : 7)
14. (600000 – 538704) * 500 : 300
15. 280 : (60 : 15) – (25 + 3 * 8) : 7 + 3 * (720 : 80)
16. (250 * 840 – 145 * 1008) : 60
17. (1000 – 832) * 715 : 30 + (104402 – 58842 : 7)